算法-排序分析
/ / 点击 / 阅读耗时 10 分钟时间复杂度
在计算机科学中,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。例如,如果一个算法对于任何大小为 n (必须比 n0 大)的输入,它至多需要 5n3 + 3n 的时间运行完毕,那么它的渐近时间复杂度是 O(n3)。
为了计算时间复杂度,我们通常会估计算法的操作单元数量,每个单元运行的时间都是相同的。因此,总运行时间和算法的操作单元数量最多相差一个常量系数。
空间复杂度
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。比如直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1) 。而一般的递归算法就要有O(n)的空间复杂度了,因为每次递归都要存储返回信息。一个算法的优劣主要从算法的执行时间和所需要占用的存储空间两个方面衡量。
稳定性
我们介绍了这么多排序算法,一直在考察它们的时间复杂度和空间复杂度。而忽略了另外一个重要的指标:稳定性。
所谓稳定性是指,如果待排序数组 a 中,有两个数 a[i] 和 a[j] 相等,并且 i < j,在排好序以后,a[i] 仍然在 a[j] 之前。那么我们就说这个排序算法是稳定的。我们回顾一下,目前掌握的所有排序方法。
冒泡排序
把小的元素往前调或者把大的元素往后调。相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,没必要再把他们交换。所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
选择排序
给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。例如,序列4 2 3 1 2, 第一遍选择第一个元素4,和后面的2交换,那么原序列中两个 2 的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。但是,我们可以通过引入额外的辅助数组使它变成稳定的排序算法。这个做为作业题留给大家去思考。
插入排序
在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
快速排序
其不稳定性是由分隔算法决定的。我们在分隔的时候没有做出稳定的保证,其不稳定性是显而易见的。而且,想把它改造成稳定性的排序算法,所付出的努力会比较大,得不偿失。所以,我们通常会把快速排序做为一种不稳定的算法。
归并排序
把序列递归地分成短序列,递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2个元素如果大小相等也不会交换,这不会破坏稳定性。接着,在短的有序序列合并的过程中,稳定也不会受到破坏,合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。所以,归并排序是稳定的排序算法。
堆排序
作为选择排序的一个特例,堆排序也是不稳定的。很容易理解,我们在调整堆的时候,假设父结点与右子结点发生了对换,那么右子结点与左子树上的相同元素的次序就会打乱。它也是不稳定的排序算法。
总结
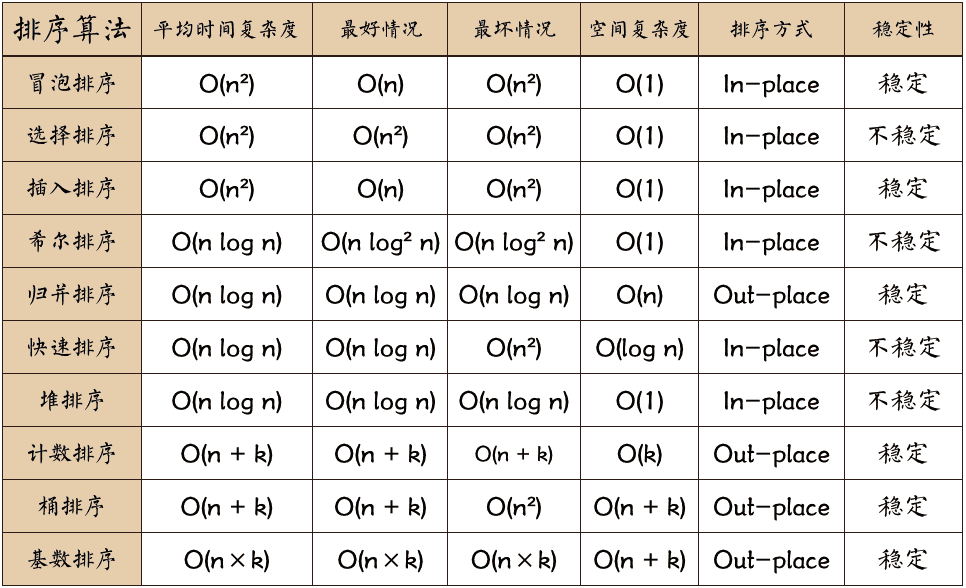
由此,我们总结了这张表: